Largest Sum Subarray (Kadane's Algorithm)

Welcome to the exciting world of Kadane's algorithm! This powerful technique swiftly finds the largest sum of a connected subarray in a list of numbers, all with the impressive speed of linear time complexity O(n).

Imagine a roller coaster ride: Each point on the track represents a number in the array, and you're seeking the section with the steepest (most positive) overall climb. That's precisely what Kadane's algorithm excels at!

package Array;

/**
 * kadanesAlgo
 */
public class kadanesAlgo {
    //Most optimal solution for Maximum Sub Array Sum.
    //Time Complexity is O(n).
    public static int kadanes(int arr[]){
        int max = Integer.MIN_VALUE;
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
            if (sum<0) {
                sum = 0;
            }
            if (sum>max) {
                max = sum;
            }
        }
        return max;
    }
    public static void main(String[] args) {
        int array[] = {-2,-3,4,-1,-2,1,5,-3};
        int max = kadanes(array);
        System.out.println("Max of Sub Array Sum is " + max);
    }
}

Let's delve into the heart of this ingenious algorithm:

1. Setting the Stage:

• We create two key players: max to track the highest sum encountered so far and sum to keep tabs on the current subarray sum.

• max is initialized to the smallest possible integer (often Integer.MIN_VALUE) to accommodate negative numbers, while sum starts from 0.

2. The Roller Coaster Journey:

• We embark on a journey through each element in the array:

  • We add the current element's value to sum.

  • If sum plummets into negative territory, it implies the current subarray isn't contributing to the maximum. So, we ditch it by resetting sum to 0. Think of it as starting a new climb from this point, as a negative sum can't lead to a higher peak.

  • If the updated sum surpasses the current max, voila! We've discovered a potentially even steeper climb. So, we replace max with this new contender.

3. Reaching the Peak:

• After traversing all elements, the final value of max represents the maximum sum achievable within any contiguous subarray in the array. This is your ultimate peak on the roller coaster ride!

Key Takeaways:

• Kadane's brilliance lies in its efficiency, processing the entire array in just one pass.

• It can handle both positive and negative elements, ensuring an accurate reflection of the terrain.

• It leverages dynamic programming, effectively building upon prior calculations for optimized results.

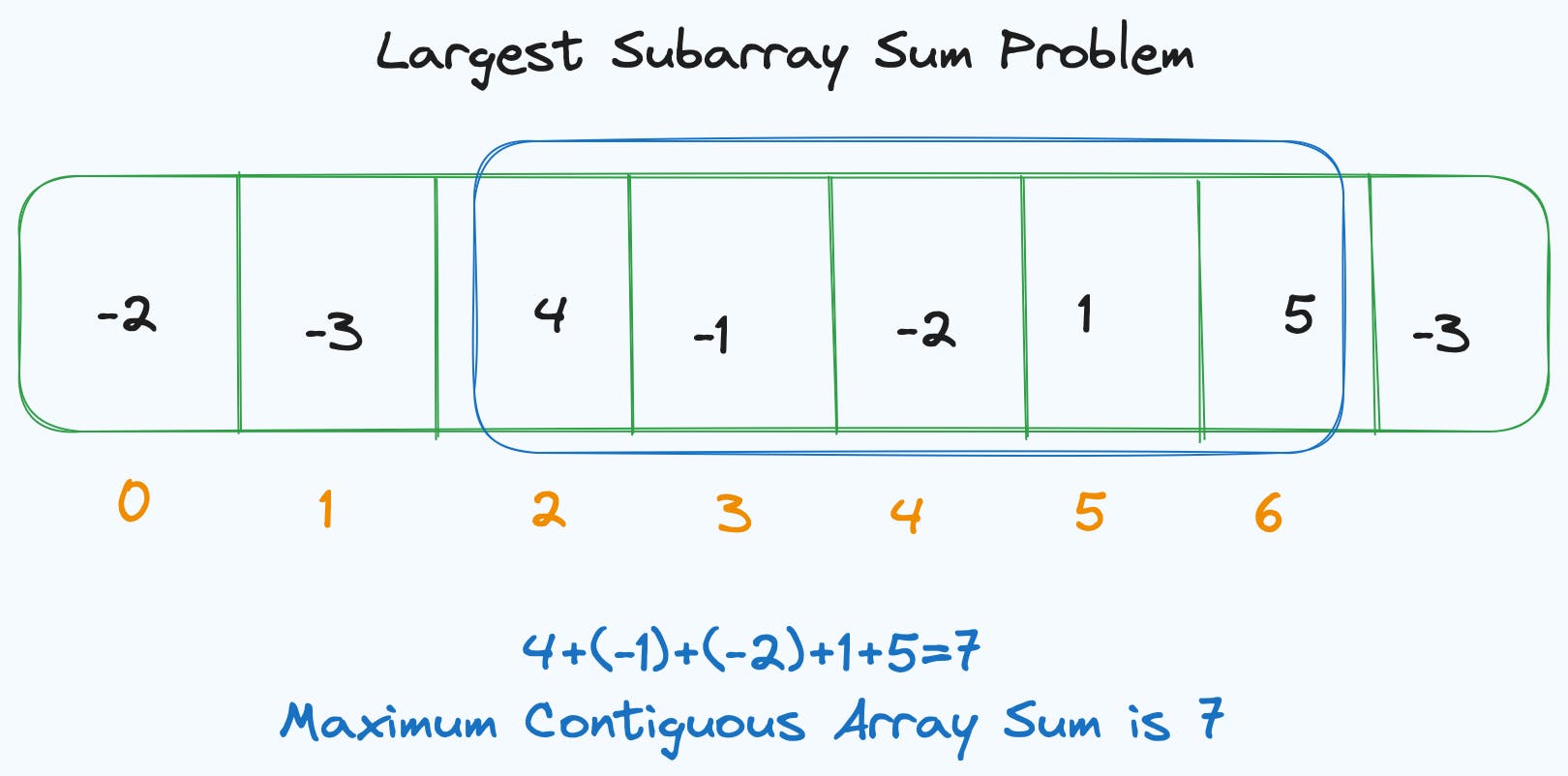
Example:

Consider the array [-2, -3, 4, -1, -2, 1, 5, -3]. Kadane's algorithm would reveal the maximum subarray sum to be 6, achieved by the subarray [4, -1, -2, 1, 5]. This translates to an exhilarating climb from 4 to 9, followed by a dip and another ascent to 6.

Conclusion: Conquering Peaks with Kadane's Algorithm

In conclusion, Kadane's algorithm stands as a testament to efficiency and understanding, enabling you to discover the maximum sum within a subarray much like an experienced explorer traversing through peaks and valleys.